Quiz-2: Mathematics and Pedagogy MCQ Questions with Answer

Mathematics and Pedagogy MCQ Questions with Answer
Quiz-1	Quiz-2	Quiz-3	Quiz-4	Quiz-5
Quiz-6	Quiz-7	Quiz-8	Quiz-9	Quiz-10
Quiz-11	Quiz-12	Quiz-13	Quiz-14	Quiz-15

Q1. If $\frac{\mathrm{x}}{\mathrm{y}}=\frac{3}{5}$ then the value of is $\frac{\mathrm{x}-\mathrm{y}}{\mathrm{x}+\mathrm{y}}$

(a) $-\frac{1}{4}$

(b) $\frac{1}{4}$

(d) -6

Answer: (a) $-\frac{1}{4}$

Solution: $\frac{\mathrm{x}}{\mathrm{y}}=\frac{3}{5}$

Using Dividendo and Componendo

$\Longrightarrow \frac{\mathrm{x}-\mathrm{y}}{\mathrm{x}=\mathrm{y}}=\frac{3-5}{3+5}=-\frac{1}{4}\,\,$

Q2. If x is a negative real number, then

(a) |xl = x

(b) | x| = –x

(d) |x| = $-\frac{1}{\mathrm{x}}$

Answer: (b) | x| = –x

Solution: Clearly, defined absolute value i.e | x| = – x

Q3. What is the maximum value of m, if the number N = 35 x 45 x 55 x 60 x 124 x 75 is divisible by 5^m?

(a) 4

(b) 5

(d) 7

Answer: (c) 6

Solution: N = 35 x 45 x 55 x 60 x 124 x 75

= 3 × 5 × 3 × 3 × 5 × 5 × 11 × 5 × 12 × 124 × 5 × 5 × 3

= 5⁶ × 3⁴ × 11 × 12 × 124

Since N is is divisible by 5^m

∴ 5^m = 5⁶ or m = 6

Q4. A student was asked to multiply a number by 25. He instead multiplied the number by 52 and got the answer 324 more than the correct answer. The number to be multiplied was

(a) 12

(b) 15

(d) 32

Answer: (a) 12

Solution: Let the number = x

52x – 25x = 324

⇒ 27x = 324

⇒x = 12

Q5. Consider the following statements:

I. No integer of the form 4k + 3, where k an integer, can be expressed as the sum of two squares.
II. The Square of an odd integer can express in the form 8k +1, where k is an integer.

Which of the statement (s) given above is/ are correct?

(a) Only I

(b) Only II

(d) Neither I nor II

Answer: (a) Only I

Solution: I. f(k) = 4k+3

For k=1, f(k) = 7; for k=2, f(k) = 11; for k=3, f(k) = 15

Values of f(k) cannot be expressed as sum of two squares for k = 1, 2, 3, …

II. f(k) = 8k+1

For k=1, f(k) = 9= 3²; for k=2, f(k) = 17; for k=3, f(k) = 25 = 5²

for k=4, f(k) = 33; for k=5, f(k) = 41

Values of f(k) is square of an odd integer only for some values of k

So, only statement I is correct

Q6. If a =$\sqrt{\left( 2013 \right) ^2+2013+2014}$, then the value of a is

(a) 1002

(b) 1007

(d) 2014

Answer: (d) 2014

Solution: $\sqrt{\left( 2013 \right) ^2+2013+2014}$

= $\sqrt{\left( 2013 \right) ^2+2.2013.1+1}$

= $\sqrt{\left( 2013+1 \right) ^2}$

= 2014

Q7. LCM of 2³ x 3 × 5 and 2⁴ x 5 x 7 is

(a) 2¹² x 3 x 5² x 7

(b) 2⁴ x 5 x 7 x 9

(d) 2³ ×3 ×5 ×7

Answer: (c) 2⁴ x 3 x 5 x 7

Solution: LCM = prime factor with highest powe = 2⁴ x 3 x 5 x 7

Q8. The value of is equal to $\frac{\left( 0.5 \right) ^4-\left( 0.4 \right) ^4}{\left( 0.5 \right) ^2+\left( 0.4 \right) ^2}$

(a) 0.9

(b) 0.09

(d) 0.009

Answer: (b) 0.09

Solution: $\frac{\left( 0.5 \right) ^4-\left( 0.4 \right) ^4}{\left( 0.5 \right) ^2+\left( 0.4 \right) ^2}$

= $\frac{\left( \left( 0.5 \right) ^2+\left( 0.4 \right) ^2 \right) .\left( \left( 0.5 \right) ^2-\left( 0.4 \right) ^2 \right)}{\left( \left( 0.5 \right) ^2+\left( 0.4 \right) ^2 \right)}$

= (0.5 + 0.4) (0.5 – 0.4) = 0.09

Q9. The sum of all interior angles of a regular convex polygon is 1080°. The measure of each of its interior angles is

(a) 108°

(b) 135°

(d) 120°

Answer: (b) 135°

Solution: sum of all interior angles of a regular convex polygon = (2n – 4)×90°

∴ (2n – 4)×90 = 1080

⇒ 2n – 4 = 12

⇒2n = 16

⇒ n = 8

∴ each interior angles of a regular convex polygon = $\frac{1080\degree}{8}=135\degree$

Q10.The mean of range, mode, and median of the data 4, 3, 2, 2, 7, 2, 2, 0, 3, 4, 4 is

(a) 4

(b) 3

(d) 2

Answer: (a) 4

Solution: Arranging the given data in a table with their frequency:

Data

Frequency

From the table Range = 7 – 0 = 7

Mode = 2 ( frequency 4)

Median = 3

∴ mean of range, mode and median = $\frac{7 +\,\,2 +3}{3}=4$

Q11. In Δ DEF and APQR, if PQ = DE, EF = PR and FD = QR, then

(a) Δ DEF ≅ Δ RPQ

(b) Δ DEF ≅ Δ QPR

(d) Δ DEF ≅ Δ PRQ

Answer: (b) Δ DEF ≅ Δ QPR

Solution:

From figure,

PQ = DE, EF = PR and FD = QR ( all given)

∴ DEF ≅ Δ QPR

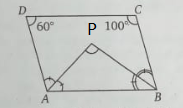
Q12. In a quadrilateral ABCD, ∠D = 60° and ∠C = 100 °. The bisectors of ∠A and ∠B meet at the point P. The measures of ∠APB is

(a) 80°

(b) 70°

(d) 60°

Answer: (a) 80°

Solution:

Let ∠A = 2x and ∠B = 2y

∴ 60° + 100° + 2x + 2y = 360 ( sum of all interior angle of quadilateral is 360°)

or x + y = 100

From Δ APB, x + y + ∠APB = 180° ( sum of all interior angle of triangle is 180°)

Or, APB = 180 – 100 (since, x + y = 100°)

∠APB = 80°

Q13. A train T leaves a place P at 5:00 a.m. and reaches another place Q at 9:00 a.m. another train T2 leaves place Q at 7:00 a.m. and reaches place P at 10:30 a.m. The time at which the two trains cross each other is

(a) 8:26 a.m.

(b) 7:56 a.m.

(d) 8:00 a.m.

Answer: (b) 7:56 a.m.

Solution: Let Distance between P and Q = x km. And the train meet each other t hour after 7:00 am

Speed of first train x/4 km/hr and distance coveer when they meet = $\frac{\left( 2+\mathrm{t} \right) \mathrm{x}}{4}$ km

Speed of 2^nd train = $\frac{2\mathrm{x}}{7}$ km/hr and distance coveer when they meet = $\frac{2\mathrm{xt}}{7}$

Now, $\frac{\left( 2+\mathrm{t} \right) \mathrm{x}}{4}+\frac{2\mathrm{xt}}{7}\,\,=\mathrm{x}$

⇒ 14 + 7t + 8t = 28

⇒ 15t = 14

⇒ t = 14/15 hr = 56 min

∴ They meet each other at 7:56 am

Q14. X can do $\frac{3}{4}$ of work in 12 days. In how many days X can finish the ½ work?

(a) 8 days

(b) 16 days

(d) 24 days

Answer: (a) 8 days

Solution: X can do $\frac{3}{4}$ of work in 12 days

X can do $\frac{1}{2}$ of a work in $\frac{12\times 4}{3\times 2}=8$ days

Q15. If after 24

(a) 70000

(b) 90000

(d) 89000

Answer: (b) 90000

Solution: the total output of the coal-mine = 100x quintals

Wastage = 24x and use full output = 76

76x = 68400

⇒ x = 900

∴ the total output of the coal-mine = 90000 quintals

Q16. A man purchased a watch for 400 and sold it at a gain of 20

(a) 300

(b) 320

(d) 500

Answer: (d) 500

Solution: Let selling price = 100x

Then, 400 + 20x = 100x

⇒ 80x = 400

⇒x = 5

∴ Selling price = 500

Q17. The ratio of ages of A and B is 2: 5 and the ratio of ages of B and C is 3: 4. What is the ratio of ages of A, B and C?

(a) 6:15:20

(b) 8: 5: 3

(d) 2: 15: 4

Answer: (a) 6:15:20

Solution: Using Ratio and Portion trick

Q18. Divide the number 26244 by the smallest number, so that the quotient is a perfect cube, so the smallest number is

(a) 4

(b) 6

(d) 16

Answer: (b) 6

Solution: $26244 =2\times 2\times 3\times 3\times \overline{3\times 3\times 3}\times \overline{3\times 3\times 3}$

∴ Required the smallest number = 2×3

Q19. When in two linear equations a₁x + b₁y = c₁ and a₂x + b₂y = C₂, $\frac{\mathrm{a}_1}{\mathrm{a}_2}\ne \frac{\mathrm{b}_1}{\mathrm{b}_2}$ then the graph is

(a) parallel

(b) intersection at one point

(d) None of the above

Answer: (b) intersection at one point

Solution: $\frac{\mathrm{a}_1}{\mathrm{a}_2}\ne \frac{\mathrm{b}_1}{\mathrm{b}_2}$ this case is unique solution. So the graph of equation will interect in a point.

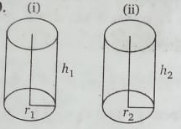
Q20. The radii of the bases of two cylinders are in the ratio of 2: 3 and their heights are in the ratio of 5:3. The ratio of their volumes is

(a) 7: 6

(b) 10: 9

(d) 20:27

Answer: (d) 20:27

Solution:

Let their ratio and height respectively = 2r, 3r and 5h, 3h

Ratio of their volume = $\frac{\frac{4}{3}\Pi \left( 2\mathrm{r} \right) ^25\mathrm{h}}{\frac{4}{3}\Pi \left( 3\mathrm{r} \right) ^23\mathrm{h}}=\frac{20}{27}=20:27$

Q21. The nature of Mathematics is

(a) logical

(b) ornamental

(d) not for common people

Answer: (a) logical

Q22. The term, ‘ Mathematical tools ‘ refers to

(a) calculators, rulers, tape measures, protractors, compass, etc.

(b) charts based on formulae and concepts, graph papers, dotted sheet, etc

(d) physical material like geo-board and 3D models, cubic rods, etc

Answer: (c) all types of materials including language, written symbols, meaningful instructions to establish their purpose

Q23. Read the following question from the class VI textbook

” Write a pair of integers whose sum gives a negative integer. ”

The above question refers to

(a) reflective question

(b) closed-ended question

(d) open-ended question

Answer: (d) open-ended question

Q24. A learner exhibiting difficulty in sorting, recognizing patterns, orienting numbers and shapes, telling time and measurement may have dyscalculia with difficulty in

(a) language processing

(b) visual-memory

(d) visual-spatial skills

Answer: (d) visual-spatial skills

Q25. In class I-VI, in the unit of Understanding Quadrilaterals, important results related to the angle-sum property of quadrilaterals are introduced using paper folding activity followed by the exercise based on these properties. At this level proof of the angle, the property is not given, as the students of class VI are at Van Hiele level of

(a) Level 2-Informal Deduction

(b) Level 1-analysis

(d) Level 0-Visualization

Answer: (a) Level 2-Informal Deduction

Q26. CBSE announced the celebration of ‘ GANIT Week in schools to commemorate the birth anniversary of the legendary mathematician, Srinivasa Ramanujan. GANIT stands for

(a) Growing Ability in Numerical Innovations and Techniques

(b) Growing aptitude in Numerical Innovations and Training

(d) Growing aptitude in Numerical Innovations and Techniques

Answer: (b) Growing aptitude in Numerical Innovations and Training

Q27. The teaching stage does not have the

(a) proactive stage

(b) interactive stage

(d) middle active stage

Answer: (d) middle active stage

Q28. The role of the intervening variable in the teaching process of mathematics is

(a) diagnostic activities

(b) remedial activities

(d) All of the above

Answer: (d) All of the above

Q29. The main aim of drill-work in mathematics is

(a) to understand new formula

(b) to enhance computation skill

(d) to clear the new concept

Answer: (b) to enhance computation skill

Q30. The appropriate method for the establishment of the formulae in Mathematics is

(a) induction

(b) planning

(d) None of these

Answer: (a) induction

For Latest Post Join our Telegram Channel

Quiz-2: Mathematics and Pedagogy MCQ Questions with Answer

Mathematics and Pedagogy MCQ Questions with Answer

Read Important Article

Leave a Comment Cancel reply

© Copyright 2020: Exam Portal