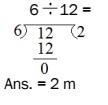Quiz-4: Math and Pedagogy MCQ Questions with Answer : Exam Portal

Math and Pedagogy MCQ Question with Answer
Quiz-1	Quiz-2	Quiz-3	Quiz-4	Quiz-5
Quiz-6	Quiz-7	Quiz-8	Quiz-9	Quiz-10
Quiz-11	Quiz-12	Quiz-13	Quiz-14	Quiz-15

Directions (Q. 1–3): Answer the following questions by selecting the most appropriate option.

Q1. In a triangle, at least two angles must be

(a) Right angles

(b) Obtuse angles

(d) None of these

Answer: (c) Acute angles

Explanation: In any triangle, at least two angles must be acute. An acute angle is an angle smaller than a right angle.

Q2. ABCD is a parallelogram in which ∠B = 80°. What is the value of ∠D?

(a) 60°

(b) 80°

(d) 50°

Answer: (b) 80°

Explanation: ABCD is a parallelogram and we know that the opposite angles of a parallelogram are equal.

∴ ∠B = ∠D = 80°

Q3. Which of the following statements is not true about a cube?

(a) A cube has 6 faces

(b) A cube has 12 edges

(d) A cube has all sides equal

Answer: (a) A cube has 6 faces

Explanation: A cube has 8 vertices, 6 faces, and 12 edges.

Q4. What will be the digit in the unit place is the product of 119, 118, 117 and 116?

(a) 4

(b) 1

(d) 0

Answer: (a) 4

Explanation: The unit digits of 119, 118, 117 and 116 are 9, 8, 7 and 6, respectively.

And 9 × 8 × 7 × 6 = 3024

The unit digit of 3024 is 4.

Therefore, the unit digit of the product of 119, 118, 117 and 116 is 4.

Q5. Which of the following numbers is divisible by 9?

(a) 254789

(b) 214357

(d) 774342

Answer: (d) 774342

Explanation: A number is divisible by 9 if the sum of the digits of the number is divisible by 9.

Sum of digits of 254789 = 2+ 5 + 4 + 7 + 8 + 9 = 35

So, it is not divisible by 9.

Sum of digits of 214357 = 2 + 1 + 4 + 3 + 5 + 7 = 22

So, it is not divisible by 9.

Sum of digits of 745321 = 7 + 4 + 5 + 3 + 2 + 1 = 22

So, it is not divisible by 9.

Sum of digits of 774342 = 7 + 7 + 4 + 3 + 4 + 2 = 27

So, it is divisible by 9.

Q6. What will be the difference between the largest and the smallest numbers formed by 0, 2 and 4?

(a) 204

(b) 18

(d) 216

Answer: (d) 216

Explanation: The largest number formed by 0, 2 and 4 = 420

The smallest number formed by 0, 2 and 4 = 204

Difference = 420 – 204 = 216

Q7. Rajshree industries sold 78000 units of a cosmetic soap brand in 2013 and 100990 units of the same soap in 2014. The increase in the number of sold cosmetic soap units in 2014 is

(a) 20990 units

(b) 21990 units

(d) 23990 units

Answer: (c) 22990 units

Explanation: Increase in number of sold cosmetic soap units in 2014 = 100990 – 78000 = 22990 units

Q8. Solve $\frac{19}{21}\times \frac{399}{323}\times \frac{476}{361}$

(a) $\frac{28}{91}$

(b) $\frac{82}{19}$

(d) $\frac{28}{19}$

Answer: (d) $\frac{28}{19}$

Explanation: $\frac{19}{21}\times \frac{399}{323}\times \frac{476}{361}\,\,=\,\,\frac{19\times 19\times 21\times 28\times 17}{21\times 19\times 17\times 19\times 19}=\frac{28}{19}$

Q9. Simplify 10 + (205 ÷ 5 – 5) ÷ 6

(a) 42

(b) 82

(d) 55

Answer: (c) 16

Explanation: 10 + (205 ÷ 5 – 5) ÷ 6

= 10 + (41 – 5) ÷ 6

= 10 + 36 ÷ 6

= 10 + 6 = 16

Q10. Which mathematical operation should come in place of “*” in the equation 24 × 26 – 18 * 2 = 615?

(a) +

(b) –

(d) ÷

Answer: (d) ÷

Explanation: 24 × 26 – 18 * 2 = 615

⇒ 624 – 18 * 2 = 615

⇒ 624 – 615 = 18 * 2

⇒ 9 = 18 * 2 = 18 ÷ 2

∴ ÷ should come in place of “*”

Q11. Which of the following lengths is equivalent to 4 cm 5 mm?

(a) 31.5 cm

(b) 45 mm

(d) 31.5 mm

Answer: (b) 45 mm

Explanation: 4 cm 5 mm = 40 mm + 5 mm = 45 mm

Q12. Which of the following relations is correct?

(a) 1 kg = 10000 g

(b) 1 mg = 0.01 g

(d) 1 mg = 0.001 g

Answer: (d) 1 mg = 0.001 g

Explanation: 1000 mg = 1 g

⇒ 1 mg = 0.001 g

Q13. The capacity of a water bottle is 3752 L. What is the capacity of the water bottle in kilolitre and litre units?

(a) 3 kL 758 L

(b) 3 kL 752 L

(d) 3 kL 552 L

Answer: (b) 3 kL 752 L

Explanation: 3752 L = 3000 L + 752 L = 3 k L 752 L

Q14. How many complete weeks are there in a year?

(a) 52

(b) 50

(d) 53

Answer: (a) 52

Explanation: We know that there are 365 days in a year.

∴ 365 days = $\frac{365}{7}=52\frac{1}{7}$ weeks

So, there are 52 complete weeks and 1 day in a year.

Q15. Which of the following numbers will replace the question mark in the pattern?

(a) 10

(b) 12

(d) 13

Answer: (b) 12

Explanation: 2 + 4 =6; 6 + 6 = 12; 12 + 8 = 20; 20 + 10 = 30

Q16. How many cubes do you see in the picture below? This question tries to evaluate the students for their

(a) Mathematical sense

(b) Geometrical and spatial sense

(d) Common sense

Answer: (b)

Explanation: This question assesses the development of a geometrical and spatial sense of the students as to whether they can make sense of number concepts related to basic maths and apply spatial relationships to organise and interpret mathematical data.

Q17. Ankit studying in Class IV was asked “Which of the two angles shown below is small?” He thought for a while and then said, “Angle A is smaller than angle B”. Based on the common misconception that children have, what could be the basis of Ankit’s answer?

(a) He must have thought that the angle having lines of shorter length is smaller.

(b) He must have measured the angles.

(d) He must have made just a quick guess.

Answer: (a)

Explanation: Most of the students at Ankit’s age feel that the size of the constituting lines makes an angle big or small. They do not know that angle is the measure of rotation. The teacher should provide hands on experiences of constructing and measuring different types of angles to make them understand this concept well.

Q18. Which type of error do you see in the following example?

(a) Error related to gaps in the knowledge of basic facts

(b) Error related to regrouping

(d) Error due to carelessness

Answer: (b)

Explanation: It is an error due to a lack of knowledge about place value and regrouping.

The table of 9 has been used correctly, but the number ‘4’ has not been carried over to the tens column.

Q19. As per NCF 2005, one of the main goals of Mathematics education in schools is to

(a) Develop numeracy skills

(b) Enhance problem-solving skills

(d) Mathematize the child’s thought process

Answer: (d)

Explanation: According to NCF 2005, one of the main goals of mathematics education in schools is to develop every child’s thought process. This is considered to be the broad aim of education.

Q20. The students of class IV are given the following puzzle to solve: Both my digits are even. The first digit is smaller than the second digit. The sum of my digits is 10. What number am I? (46 or 56?) What is the objective of giving such puzzles to the students?

(a) To provide them with an interesting and challenging environment

(b) To assess whether they understand the terms even and odd

(d) To test the comprehension level of the students

Answer: (a)

Explanation: Puzzles are interesting and challenging for students. They provide an opportunity to understand the language used, analyse the conditions given and think of the solution. Critical thinking is required to arrive at the answer.

Q21. The students of class IV have been given the assignment to prove with the help of suitable figures that there can be two or more rectangles having the same perimeter (for example, 24 cm). The rubric for assessing the work of a student should be on whether he/she is able to

(a) make two rectangles having a perimeter equal to 24 cm

(b) write down all possible combinations of lengths and breadths of rectangles in order to get the same perimeter and draw two of them with accurate measurements

(d) write down different combinations of lengths and breadths of rectangles in order to get the same perimeter

Answer: (b)

Explanation: The rubric stated in option (b) is the clearest and specific among the four options. Teachers should use such assessment tasks as they encourage the use of mathematical practices by students.

Q22. The nature of mathematics is

(a) Ornamental

(b) Difficult

(d) Uncommon

Answer: (c)

Explanation: The discipline of maths has a logical structure because its most fundamental concepts include numbers, symbols, shapes, algorithms, axioms, theorems, proofs, etc., the understanding of which requires critical thinking and reasoning.

Q23. Manu loves to recite tables loudly. He enjoys discussions, debates and talking to others but has difficulty in working silently on maths problems. Manu is a/an

(a) Hyperactive child

(b) Kinaesthetic learner

(d) Visual learner

Answer: (c)

Explanation: Manu is an auditory learner. Auditory learners like to read aloud, are more adept at giving oral responses and usually cannot sit quietly for long.

Q24. Preeti learns better when taught through charts, models or other visuals. She has difficulty in understanding the written matter. Preeti is a/an

(a) Auditory learner

(b) Visual learner

(d) Slow child

Answer: (b)

Explanation: Preeti is a visual learner. Such learners have their visual receptors uniquely at work. They learn best by seeing and can notice even those details in the surroundings that others might miss. However, they often struggle with sequencing letters or numbers for meaning, which affects their reading and writing skills.

Q25. Reena was asked to solve the problem “One ant has 6 legs. How many legs do 25 ants have?” Her response was 31 legs. What could be the reason for her wrong answer?

(a) Lack of comprehension

(b) Lack of knowledge of basic facts

(d) Carelessness

Answer: (c)

Explanation: Reena used the wrong operator. She should have multiplied 25 by 6, but instead, she added them.

Q26. Salim was given a problem sum “A 6 m ribbon has to be cut into 12 pieces. What will be the length of each piece?” This is how he solved it: 6 ÷ 12 = 2 m (ans). What is wrong with Salim’s solution?

(a) Lack of knowledge of basic facts

(b) Wrong transformation

(d) Lack of attention

Answer: (b)

Explanation: The wrong transformation is the reason. Salim read the problem and understood it.

He wrote 6 ÷ 12, which is correct, but instead of dividing 6 m into 12 pieces, he divided 12 m into 6 pieces.

Q27. The ability of a child to sort and arrange different objects, such as pictures, in an orderly manner is called

(a) Conservation

(b) Assimilation

(d) Seriatim

Answer: (d)

Explanation: The ability to seriate, i.e. to know that the biggest comes after bigger, which follows big, develops step by step. However, it is dependent upon the individual developmental rates of children.

Q28. Who opposed Piaget’s cognitive stages of development and felt that schools waste time trying to match the complexity of subject material to a child’s cognitive stage of development?

(a) Vygotsky

(b) Bruner

(d) Ausubel

Answer: (b)

Explanation: Bruner believed that a child of any age is capable of understanding complex information. He suggested that this was possible through the concept of the spiral curriculum in which the information is structured in such a way that complex ideas are taught at a simplified level first and then re-visited at more complex levels later on. He believed that if children are taught in this way, they develop the ability to solve problems by themselves.

Q29. From the chapter ‘Tenths and Hundredths’ of Class V, the teacher asked the students to convert lengths given in millimetres into centimetres and vice versa. This question refers to

(a) higher level of thinking

(b) the lower level of thinking

(d) spatial thinking

Answer: (b)

Explanation: Lower order thinking skills are knowledge, understanding and application, whereas higher-order thinking skills are analysis, evaluation and creation. ‘To convert’ comes under the understanding or comprehension category and is a lower order thinking skill.

Q30. Students that need “hands-on experiences and use of manipulative like pattern blocks, Cuisenaire rods, algebra tiles, algebra cubes, geoboards, tangrams, counters, dice, etc.,” are at the

(a) Sensorimotor stage

(b) Concrete operational stage

(d) Formal operational stage

Answer: (b)

Explanation: Students needing these aids for learning are at the concrete operational stage, according to Piaget. Most students at the primary level undergo this stage, which is marked by the beginning of the logical or operational thinking process.

Math and Pedagogy MCQ Question with Answer

Leave a Comment Cancel reply