Math and Pedagogy MCQ Question with Answer | ||||
| Quiz-1 | Quiz-2 | Quiz-3 | Quiz-4 | Quiz-5 |
| Quiz-6 | Quiz-7 | Quiz-8 | Quiz-9 | Quiz-10 |
| Quiz-11 | Quiz-12 | Quiz-13 | Quiz-14 | Quiz-15 |
Directions (Q. 1–30): Answer the following questions by selecting the most appropriate option.
Q1. An angle that is more than 90° but less than 180° is called
(a) an acute angle
(b) a right angle
(c) an obtuse angle
(d) a reflex angle
| Answer: (c) Explanation: An angle whose measure is more than 90° and less than 180° is called an obtuse angle. |
Q2. Which of the following is not a polyhedron?
(a) Cube
(b) Cuboid
(c) Sphere
(d) Tetrahedron
| Answer: (c) Explanation: In a sphere, there are no edges or vertices |
Q3. The length, breadth and height of a cuboid are 5 cm, 4 cm and 3 cm, respectively. What will be the total surface area of the cuboid?
(a) 94 cm2
(b) 94 cm3
(c) 47 cm3
(d) 47 cm2
| Answer: (a) Explanation: Total surface area of cuboid = 2(l×b + b×h + h×l) = 2(5 × 4 + 4 × 3 + 3 × 5) = 2(20 + 12 + 15) = 2 × 47 = 94 cm2 |
Q4. ABCD is a parallelogram. If ∠AOD 75, the values of x, y and z are
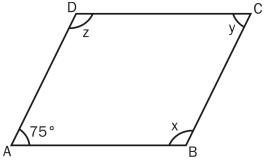
(a) 105°, 75°, 105°
(b) 105°, 105°, 75°
(c) 75°, 75°, 105°
(d) 105°, 75°, 75°
| Answer: (a) Explanation: Two consecutive angles of a parallelogram are supplementary. Therefore, 75° + x = 180° ⇒ x = 180° – 75° = 105° We know that opposite angles of a parallelogram are equal. Therefore, y = 75° and z = 105° |
Q5. The unit digit of the square of 17548216 is
(a) 8
(b) 6
(c) 4
(d) 2
| Answer: (b) Explanation: The unit digit of the square of a number ending with 6 will be always 6 |
Q6. If a bus covers 35.25 km in 2.5 hours, the speed of bus is
(a) 14.12 km/h
(b) 14.21 km/h
(c) 88.125 km/h
(d) 14.1 km/h
| Answer: (d) Explanation: Speed = $\frac{Distance}{Time}$ = $\frac{35.25}{2.5}=14.1$ km/h |
Q7. Find the largest three-digit number exactly divisible by 12, 18 and 20.
(a) 990
(b) 900
(c) 980
(d) 920
| Answer: (b) Explanation: The largest three-digit number is 999. LCM of 12, 18 and 20 is 180. Dividing 999 by 180 leaves a remainder of 99. Required number = 999 – 99 = 900 |
Q8. The sum of all the positive factors of 24 is
(a) 30
(b) 144
(c) 60
(d) 120
| Answer: (c) Explanation: Positive factors of 24 are 1, 2, 3, 4, 6, 8, 12, and 24 Sum = 1 + 2 + 3 + 4 + 6 + 8 + 12 + 24 = 60 |
Q9. What is the difference between the largest and smallest numbers formed by 3, 5 and 7?
(a) 396
(b) 404
(c) 693
(d) 0
| Answer: (a) Explanation: The largest number formed by 3, 5 and 7 = 753 The smallest number formed by 3, 5 and 7 = 357 Difference = 753 – 357 = 396 |
Q10. If 1×6543 is divisible by 9, then what is the value of x?
(a) 8
(b) 4
(c) 2
(d) 1
| Answer: (a) Explanation: A number is divisible by 9 if the sum of its digits is divisible by 9. Sum of digits of 1×6543 = 1 + x + 6 + 5 + 4 + 3 = x + 19 x + 19 will be divisible by 9 if x becomes 8 and x + 19 becomes 27. |
Q11. Reema bought 54 m 15 cm of cloth. From this, 15 m 5 cm of cloth was used to make curtains. How much cloth is left now?
(a) 39 m 10 cm
(b) 39.01 m
(c) 391 cm
(d) 3910 m
| Answer: (a) Explanation: 54 m 15 cm – 15 m 5 cm = 39 m 10 cm |
Q12. 3 kg 500 g + 7 kg 700 g + 5 kg 900 g =
(a) 15 kg 140 g
(b) 16 kg 140 g
(c) 17 kg 100 g
(d) 16 kg 100 g
| Answer: (c) Explanation: 3 kg 500 gm. + 7kg 700 gm. + 5 kg 900 gm. = 17 kg 100 gm |
Q13. What is the value of the expression 19 dl 7 ml × 7?
(a) 133 dL 7 mL
(b) 113 dL 49 mL
(c) 19 dL 49 mL
(d) 133 dL 49 mL
| Answer: (d) Explanation: 19 dL 7 mL × 7 = 133 dL 49 mL |
Q14. How many sides does a regular polygon have if each angle is of measure 108°?
(a) 5
(b) 8
(c) 6
(d) 7
| Answer: (a) Explanation: Since the given polygon is regular, it’s all angles are equal. And, $\frac{n-2}{n}\times 180\degree=108\degree$ (where n is the number of sides of the polygon) On solving, we get n = 5. |
Q15. ABC represents “I am the police,” BCD represents “I am a doctor” and BE represents “I went.” Which of the following letters stands for “am”?
(a) B
(b) D
(c) E
(d) A
| Answer: (a) Explanation: Common between ABC and BE is “B” and common between “I am police” and “I went” is “I”. Hence, “I” is represented by “B”. |
Q16. The students of Class V have been given the activity “How many unit cubes are required to make a cube of 2×2×2?” The main objective of giving this activity to the students is to

(a) Create interest of the students in mathematics
(b) Create cubes of different sizes
(c) Estimate the number of unit cubes that can fit in a bigger cube
(d) Develop mathematical vocabulary
| Answer: (c) Explanation: Enabling the students to estimate the number of unit cubes that can fit in a bigger cube is the main objective of this type of activity. Such activities develop children’s spatial understanding relating to geometrical shapes. |
Q17. Angles can be a difficult geometric concept for students. To help students understand the concept of angles, what should be the sequence of the following activities?
(i) Introducing the concept of acute and obtuse angles through paper folding, geoboards, dot papers, etc.
(ii) Showing angles in familiar things
(iii) Using informal units to compare angles (straight, right, acute and obtuse)
(iv) Explaining the concept of right angles, straight angles and half right angles using manipulative like two sticks or two strips of tagboard, paper folding, dot papers, etc.
(v) Measuring angles with formal measuring tools like protractors
(a) iii, i, ii, v, iv
(b) iv, i, v, iii, ii
(c) ii, iv, i, iii, v
(d) i, ii, iii, iv, v
| Answer: (c) Explanation: While teaching, one should always start from familiar and concrete to unfamiliar and abstract. For example, to effectively teach the mathematical concept of angles, the focus should be on developing the understanding of angles. Measurement should come at the end. |
Q18. Rajat was given an additional sum and this is how he solved it:
What could be the reason for this?
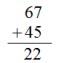
(a) Rajat has not been able to develop a good number sense and therefore could not add the numbers correctly.
(b) It seems that Rajat has used an incorrect operation (subtraction in place of addition) due to carelessness.
(c) Rajat has a very low level of intelligence. He cannot learn mathematics.
(d) Lack of practice is the main cause of this mistake. Rajat should practice hard.
| Answer: (b) Explanation: Rajat has used an incorrect operation. In place of addition, he did subtraction. Rajat should be asked to be careful and look at the signs seriously before starting to solve the sum. |
Q19. Leela was asked to solve a division sum. She solved it as follows:
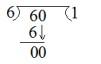
Ans. 60 ÷ 6 = 1
Leela forgot to write 0 in the quotient.
What type of error is this?
(a) Defective algorithm
(b) Basic fact error
(c) Incorrect operation
(d) Careless error
| Answer: (d) Explanation: It is a careless error. Leela knows the algorithm but has done a careless mistake of not putting 0 in the quotient. |
Q20. A teacher wants her students to be able to prepare bills for purchased vegetables and fruits and calculate prices for quantities infractions (½ kg, ¼ kg). The best method of doing this would be
(a) Written assignment
(b) Survey
(c) Discussion
(d) Roleplay
| Answer: (d) Explanation: Roleplay would be best suited for this purpose as students will find the activity related to their daily life experiences. They will learn to communicate in mathematical terms; calculate the amount of money to be paid for different quantities, some of them in fractions (onion 2 kg, ladyfinger ½ kg, green chillies ¼ kg, etc.); and, while doing so, also enjoy enacting the play. |
Q21. A student converted a mixed number into a fraction as follows:
$7\frac{3}{4}=\frac{14}{4}$
What could be the cause of this error?
(a) The student has carelessly added 7, 4 and 3 and has written the fraction as $\frac{14}{4}$
(b) He does not understand the value of 7 in the mixed number.
(c) The student does not have any number sense at all.
(d) The student does not know how to convert a mixed number into a fraction.
| Answer: (d) Explanation: The student does not know how to convert a mixed number into a fraction. This concept is usually difficult for some students. Hands on activities in the classroom can help such students to be efficient in converting mixed numbers into fractions and vice versa. |
Q22. Lalit is able to solve all addition and subtraction sums, but he often forgets to carry over numbers while adding and to deduct the borrowed number while subtracting. The best remedial strategy to remove these errors is
(a) punishing Lalit for every mistake he commits
(b) rewarding Lalit for every correct answer
(c) giving Lalit a long worksheet to practice the sums of carrying over and borrowing
(d) asking Lalit to be cautious while carrying over and borrowing and do self-checking to ensure that his answer is correct
| Answer: (d) Explanation: Though punishments and rewards may help sometimes, a habit of working carefully and ensuring that the sums are correctly solved can be developed through practice. The habit of self-checking the answers helps minimise such errors. |
Q23. Prasad has added 55 to 67 in the following manner:

What is wrong with this?
(a) Prasad has a problem in regrouping.
(b) Prasad has done this due to carelessness.
(c) Prasad has added the digits from left to right.
(d) Prasad lacks the knowledge of basic facts.
| Answer: (c) Explanation: Prasad has added the digits from left to right, whereas it should be from right to left when numbers are added in columns. He needs a proper understanding of the correct procedures of addiction, the concept of place value and a lot of practice. |
Q24. Ramesh was not able to understand division problems. So, to teach division by 4, his teacher asked him to take out four marbles at a time and see how many times he is doing it to divide all the marbles. He repeated the activity with other numbers also and understood the concept. Ramesh
(a) is a visual learner
(b) needs personal attention
(c) is an auditory learner
(d) is a kinaesthetic learner
| Answer: (d) Explanation: Ramesh is a kinaesthetic learner. Such learners learn by touching and doing things. Their tactile sense is stronger. If manipulative like marbles, pebbles, beads, blocks, etc., are used, they learn better. |
Q25. A teacher assigned the students of Class V activity of finding different types of trees, their names and the total number growing in their colony. She asked the students to make tallies for counting purposes and then make a smart chart of them. This activity has been suggested in the book mainly for the purpose of
(a) helping the students communicate with one another and enjoy the learning process
(b) helping the students to make connections between mathematical concepts and real life
(c) teaching the students through a project approach
(d) enhancing the reasoning power of the students
| Answer: (c) Explanation: This activity aims to help the students learn through a project approach. The students will visit their respective colonies in teams, try to find the names of the trees over there and collect data, and organise and present it in the form of a smart chart. It will also help the students make connections between mathematical concepts and real life. They will develop the habit of keeping themselves aware of the things around them. |
Q26. Which of the following problems from a textbook of Class IV refers to a multidisciplinary problem?
(a) Find the length, breadth and height of a brick.
(b) Find the life spans of different animals.
(c) Make designs using a compass and circular objects.
(d) Draw a line of symmetry in a given geometrical figure.
| Answer: (b) Explanation: The multidisciplinary problem given here is related to environmental studies and mathematics. The student will collect data about the life spans of different animals from books, encyclopaedias and the Internet. |
Q27. Rajni, studying in Class II, finds it difficult to differentiate between operation symbols. In place of subtraction, she would do multiplication, subtraction in place of division and so on. She also finds difficulty in reading time on the clock. Rajni has a problem with her
(a) Auditory memory
(b) Working memory
(c) Visual processing
(d) Language processing
| Answer: (c) Explanation: Students like Rajni have difficulty in visual processing. They are unable to memorise and discriminate numbers and operation symbols and use number-represented objects such as coins, clocks, calculators, phone dials, etc. Sometimes, they cannot even differentiate between left and right. They also have difficulty in manipulating simple visual patterns or maintaining their orientation to see things in space and estimating or comparing visual lengths or distances without measuring them. |
Q28. For assessing the performance of Class-III students in solving problem sums and selecting the right operation for their solution, the most appropriate rubric is: The student is able to
(a) understand the problem, and select and applies the right operation to solve it
(b) understand the language of the problem sum and identify the operations to be performed
(c) understand and solve the problem
(d) Solve the problem in a correct way
| Answer: (b) Explanation: Problem sums in mathematics pose a challenge to students because they require students to read and understand the text of the problem and create a numerical equation in solution. |
Q29. Which one of the following activities is not appropriate for data representation and data interpretation?
(a) Project
(b) Newspaper report
(c) Survey
(d) Debate
| Answer: (d) Explanation: Data representation involves collecting, analysing and presenting data. On the other hand, data interpretation means deriving meaning from the data thus represented. Data can be represented and interpreted better if the information or statistics are illustrated by diagrams, tables or graphs, as in surveys, projects, newspaper reports, etc. Such type of illustration is not possible with debates, as they are more of a discussion or an argument at the formal level. |
Q30. To assess the competence of Class-III students in the addition of 3-4 digit numbers with carrying over and regrouping, the best rubric is: The students
(a) can add two numbers correctly
(b) can add two numbers with carrying over
(c) can add 3-4 digit numbers with regrouping
(d) can add two numbers of 3-4 digits each with regrouping and without any mistake
| Answer: (d) Explanation: Students should be able to describe and apply mental mathematical strategies for adding two 3-4 digit numbers. |
