Math, Science and Pedagogy MCQ Question with Answer

Math, Science and Pedagogy MCQ Question with Answer
Quiz-1	Quiz-2	Quiz-3	Quiz-4	Quiz-5
Quiz-6	Quiz-7	Quiz-8	Quiz-9	Quiz-10
Quiz-11	Quiz-12	Quiz-13	Quiz-14	Quiz-15

Q1. The value of $\frac{2.48\times 2.48–1.52\times 1.52}{0.96}$ is

(a) 4

(b) 0:96

(d) 15.04

Answer: (a) 4

Solution:$\frac{2.48\times 2.48–1.52\times 1.52}{0.96}$

= $\frac{\left( 2.48+1.52 \right) \left( 2.48-1.52 \right)}{\left( 2.48-1.52 \right)}$ {Using formula (a² – b² = (a+b)(a–b) }

= 4

Q2. 1f $\frac{\mathrm{a}}{4}=\frac{\mathrm{b}}{5}=\frac{\mathrm{c}}{6}$ then the value of $\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{\mathrm{b}}$

(a) 3

(b) 2

(d) 4

Answer: (a) 3

Solution: $\frac{\mathrm{a}}{4}=\frac{\mathrm{b}}{5}=\frac{\mathrm{c}}{6}\,\,=\,\,\mathrm{k}$

∴ a = 4k, b=5k, c=6k

∴$\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{\mathrm{b}}$

= $\frac{4\mathrm{k}+5\mathrm{k}+6\mathrm{k}}{5\mathrm{k}}\,\,=\,\,\frac{15\mathrm{k}}{5\mathrm{k}}\,\,=3$

Q3. If n is a natural number than $\sqrt{\mathrm{n}}$ is

(a) Always a whole number

(b) Always a natural number

(d) Always an irrational number

Answer: (c) sometimes a natural number and sometimes an irrational number

Solution: $\sqrt{3}$, $\sqrt{9}=3$ Where 9 and 3 are natural number

$\sqrt{3}$is irrational number

Q4. If $\sqrt{5}$ =2.24, then the value of $\frac{3\sqrt{5}}{2\sqrt{5}-0.48}$

(a) 1.68

(b) 16.8

(d) 0.168

Answer: (a) 1.68

Solution: $\frac{3\sqrt{5}}{2\sqrt{5}-0.48}$

= $\frac{3\times 2.24}{2\times 2.24-0.48}=1.68$

Q5. The greatest fraction out of $\frac{2}{5},\frac{5}{6},\frac{11}{12}\,\,\mathrm{and} \frac{7}{8}$

(a) 7/8

(b) 5/6

(d) 2/5

Answer: (c) 11/12

Solution: LCM of 8, 6, 12, 5 = 120

Now, $\frac{7}{8}\times 120=105$;

$\frac{5}{6}\times 120=100$;

$\frac{11}{12}\times 120=110$;

$\frac{2}{5}\times 120=48$

Clearly greatest fraction is 11/12

Q6. The line 3x – 5y = 10 cuts Y-axis at

(a) (0, 2)

(b) (0, 1)

(d) (0, 4)

Answer: (a) (0, 2)

Solution: at Y-axis x=0, put the value of x in equation

3.0 – 5y = 10

⇒ 5y = 10 or y = 2

Required point on y-axis (0, 2)

Q7. If x = 2³ x3² x 5⁴ and y = 2² x3² x5 x7, then HCF of x and y is

(a) 180

(b) 360

(d) 35

Answer: (a) 180

Solution: x = 2³ x3² x 5⁴

y = 2² x3² x5 x7

HCF of x and y = Highest common factor of x and y = 2²×3²×5 = 180

Q8. The expression $\left[ \left( \sqrt{2} \right) ^{\sqrt{2}} \right] ^{\sqrt{2}}$ gives

(a) a natural number

(b) an integer and not a natural number

(d) a real number but not a rational number

Answer: (d) a real number but not a rational number

Q9. Three numbers are in the ratio 3 : 2 : 5 and the sum of their squares is 1862. What are the three numbers?

(a) 18, 12, 30

(b) 24, 16, 40

(d) 21,14, 35

Answer: (d) 21,14, 35

Solution: Let three numbers are 3k, 2k, and 5k

According to question,

9k² + 4k² + 25k² = 1862

⇒ k² = 1862/38 = 49

k = 7

Three numbers are 21, 14, and 35

Q10. A man sells fans at the same price on one his gain 20% and losses 20% on ‘ the other. His gain or loss is:

(a) 4% loss

(b) 4% gain

(d) 1% loss

Answer: (a) 4% loss

Solution: In these case always loss = $\frac{20\times 20}{100}=4%$

Q11. A rise of 25% in the price of grapes compels a person to buy 1.5 kg of grapes less for Rs. 240. Then, the original price of grapes per kg is

(a) Rs. 40

(b) Rs. 32

(d) Rs. 28

Answer: (b) Rs. 32

Solution: Using tricks,

The original price of grapes = $\frac{240\times 25}{\left( 100+25 \right) \times 1.5}=32$

See Trick=> Click Here

Q12. 7 men and 8 boys can do a piece of work in 2 days. 4 men and 12 boys can do 29/56 of the same work in 1 day. In how many days will 1 man do this work?

(a) 24 days

(b) 25 days

(d) 28 days

Answer: (d) 28 days

Solution: Let one man can complete the work in m days and one boys can b days

According question, $\frac{7}{\mathrm{m}}+\frac{8}{\mathrm{b}}=\frac{1}{2}$

⇒$\frac{21}{\mathrm{m}}+\frac{24}{\mathrm{b}}=\frac{3}{2}$ (multiplying 3 both side) —– (i)

and $\frac{4}{\mathrm{m}}+\frac{12}{\mathrm{b}}=\frac{29}{56}$

⇒$\frac{8}{\mathrm{m}}+\frac{24}{\mathrm{b}}=\frac{29}{28}$( multiplying 2 both side) —– (ii)

we get (i) – (ii)

⇒$\frac{21}{\mathrm{m}}-\frac{8}{\mathrm{m}}=\frac{3}{2}-\frac{29}{28}$

⇒$\frac{13}{\mathrm{m}}=\frac{13}{28}$

⇒ m = 28

Q13. A train passes telegraph post in the 40s moving at a rate of 36 km/h. Then, the length of the train is

(a) 400 m

(b) 500 m

(d) 395 m

Answer: (a) 400 m

Solution:

Speed of train = $36\times \frac{5}{18}=10\,\,\mathrm{m}/\mathrm{s}$

Length of the train = 40 × 10 = 400 Metre

Q14. 1n figure determines the value of y.

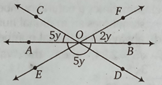
(a) 25°

(b) 35°

(d) 40°

Answer: (c) 15°

Solution: AOB is straight line, ∠AOC +∠COF +∠FOB = 180

⇒ ∠AOC +∠COF + ∠EOD = 180 (∠FOB = ∠EOD opposite angle)

⇒ 5y + 5y + 2y = 180

⇒ y = 15

Q15. If the arms of one angle are respectively parallel to the arms of another angle, then the two angles are

(a) Neither equal nor supplementary

(b) Not equal but supplementary

(d) Either equal or supplementary

Answer: (b) not equal but supplementary

Solution: If the arms of one angle are respectively parallel to the arms of another angle, then the two angles not equal but supplementary

Line l₁ || Line l₂

then ∠1 ≠ ∠2 but ∠1 + ∠2 = 180°

Q16.1n the given figure, ABC is a triangle, BC is parallel to AE. If BC = AC, then what is the value of ∠CAE?

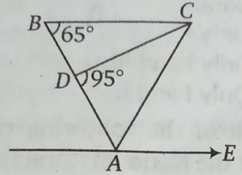
(a) 20°

(b) 30°

(d) 50°

Answer: (d) 50°

Solution: Given that, BC || AE

∴ ∠CAB + ∠BAE = 180°

∠BAE = 180° – 65° = 115°

Again, BC = AC

∴∠CAB = ∠ ABC = 65°

∴∠CAE = 115° – 65° = 50°

Q17. ABCD is a trapezium in which AB || CD and AB = 2CD. Its diagonals intersect each other at 0, then the ratio of the ‘areas of the Δ A0B and Δ COD is

(a) 1 : 2

(b) 2 : 1

(d) 1 : 4

Answer: (c) 4 : 1

Solution:

Let PQ be the perpendicular distance between the two parallel sides AB and CD

AB = 2CD, ∴ OP = 2OQ

So, $\frac{\mathrm{Area} \mathrm{of} \Delta \mathrm{AOB}}{\mathrm{Area} \mathrm{of} \Delta \mathrm{COD}}$

= $\frac{\frac{1}{2}\times \mathrm{OP}\times \mathrm{AB}}{\frac{1}{2}\times \mathrm{OQ}\times \mathrm{CD}}$

= $\frac{\frac{1}{2}\times 2\mathrm{OQ}\times 2\mathrm{CD}}{\frac{1}{2}\times \mathrm{OQ}\times \mathrm{CD}}$

= $=\frac{4}{1}=4:1$

Q18. In a circle of radius 17 cm, two parallel chords are drawn on the opposite sides of a diameter. The distance between the chords is 23 cm. If the length of one chord is 16 cm, then the length of the other chord is

(a) 34 cm

(b) 15 cm

(d) 30 cm

Answer: (d) 30 cm

Solution:

Here, BE =$\frac{1}{2}\mathrm{AB}=\frac{16}{2}=8\,\,\mathrm{cm}$

OB = OD = 17 cm

In right angled ΔOEB,

OE = $\sqrt{\mathrm{OE}^2-\mathrm{BE}^2}$

= $\sqrt{17^2-8^2}\,\,=15$

∴ OF = EF – OE = 23 – 15 = 8

In right angled ΔOFD,

FD = $\sqrt{\mathrm{OD}^2-\mathrm{OF}^2}$

= $\sqrt{17^2-8^2}=15$

∴ Length of other chord = 2FD = 15×2 = 30

Q19. The given graph here shows the production of food grains of a country in different years. Find the percentage 1 increases in production from 1984 to 1985

(a) 15

(b) 30

(d) 100

Answer: (d) 100

Q20. Which one is correct for the following data?

–1, 3, 2, 0, 1 6, 8, 5, 10, 11, 5

(a) Mean = Median = Mode

(b) Mean =Mode

(d) Mean =5

Answer: (c) Mode = Median

Solution: Given, –1, 3, 2, 0, 1 6, 8, 5, 10, 11, 5

Mean = $\frac{-1+3+2+0+1+6+8+5+10+11+5}{11}=4.54545$

Arranging in ascending order, –1, 0, 1, 2, 3, 5, 5, 6, 8, 10, 11

n= 11

Median = $\frac{\mathrm{n}+1}{2}$ = $\frac{11+1}{2}$ = 6^th term

Median = 5

Also mode = 5

∴ Median = mode

Q21.Which point is not included in the professional skills of a teacher?

(a) Self-knowledge

(b) To experiment well

(d) Satisfactory knowledge of the social matter

Answer: (d) Satisfactory knowledge of the social matter

Q22. ‘Correlation indicates a joint relationship between two variables.

(a) Ferguson

(b) Lathrop

(d) Crowder

Answer: (b) Lathrop

Q23. Characteristics of a good textbook of Mathematics should be

(a) there are many solved examples and some questions of exercise

(b) there are sufficient solved illustrations and more questions of exercise

(d) All of the above

Answer: (b) there are sufficient solved illustrations and more questions of exercise

Q24. ” Mathematics is a way to settle in the mind the habit of reasoning” has been said by

(a) Napoleon

(b) Locke

(d) Plato

Answer: (b) Locke

Q25. The main function of teaching during the interactive stage is

(a) to realise the size of the class

(b) to diagnose the difficulties

(d) All of the above

Answer: (d) All of the above

Q26. Which one of the following is not a characteristic of Mathematics learning?

(a) Change of behaviour

(b) Environmental origin

(d) All of the above

Answer: (d) All of the above

Q27. Which of the following is not an activity-based teaching method?

(a) Demonstration method

(b) Observation method

(d) Lecture method

Answer: (d) Lecture method

Q28. To be good in Mathematics, one needs to

(a) have mastery over calculations

(b) create and formulae problems through abstract thinking and logical reasoning

(d) remember solutions

Answer: (b) create and formulae problems through abstract thinking and logical reasoning

Q29. When introducing mensuration, a teacher writes all the formulae on the board before proceeding further. This reflects that she is following the

(a) deductive approach

(b) experimental approach

(d) inductive approach

Answer: (a) deductive approach

Q30. A teacher in grade-VI provided each child with a centimetre grid paper and a pair of scissors. She wanted them to explore how two-dimensional shapes can be folded into three-dimensional objects. Which of the following concepts are the students exploring?

(a) Reflection

(b) Nets

(d) Rotation

Answer: (b) Nets

Pages: 123

Pages ( 1 of 3 ): 1 2 3 Next »

For Latest Post Join our Telegram Channel

Math, Science and Pedagogy MCQ Question with Answer

Math, Science and Pedagogy MCQ Question with Answer

Read Important Article

Leave a Comment Cancel reply

© Copyright 2020: Exam Portal