Ratio and Proportion MCQ Question with Details Solution |
Read: Concept and Short Trick |
Q11. If 2A = 3B = 4C, then find A : B : C
(a) 2 : 3 : 4
(b) 4 : 3 : 2
(c) 6 : 4 : 3
(d) 3 : 4 : 6
| Answer: (c) 6 : 4 : 3 Solution: 2A = 3B = 4C = k (let) A = k2 ; B =k3; C = k4 A : B : C = k2:k3:k4=12:8:6=6:4:3 Using Trick: A : B : C = 12:13:14=6:4:3 Trick: If xA = yB = zC, then find A : B : C = 1x:1y:1z |
Q12. The total number of students in a school is 8670. If the number of boys in the school is 4545, then what will be the ratio of the total number of boys to the total number of girls in the school?
(a) 303 : 275
(b) 275 : 303
(c) 11 : 12
(d) 12 : 11
(e) None of the above
| Answer: (a) 303 : 275 Solution: Total number of student = 8670 Boys = 4545 ∴ Girls = 8670 – 4545 = 4125 Ratio of the total number of boys to the total number of girls in the school = 4545:4125 = 303:275 |
Q13. In a class, the number of boys and girls is in the ratio of 4 : 5. If 10 more boys join the class, the ratio of numbers of boys and girls becomes 6 : 5. How many girls are there in the class?
(a) 20
(b) 30
(c) 25
(d) Couldn’t be determined
(e) None of the above
| Answer: (c) 25 Solution: Boys : Girls = 4:5 ∴ Boys = 4k, Girls = 5k, k = ratio constant 10 more boys join the class Now, 4k+105k=65 ⇒ 30k = 20k+50 ⇒10k = 50 or k = 5 Numbers of girl = 25 |
Q14. What is the least integer which when added to both terms of the ratio 5 : 9 will make a ratio greater than 7 : 10?
(a) 6
(b) 8
(c) 5
(d) 7
| Answer: (c) 5 Solution: let x will added both. Now, 5+x9+x=710 ⇒ 50 + 10x = 63 + 7x ⇒ 3x = 13 or x = 133 Since x is the least integer. ∴x⩾133orx=5 |
Q15. 465 coins consists of 1 rupee, 50 paisa and 25 paisa coins. Their values are in the ratio 5: 3 : 1. The number of each type of coins respectively is
(a) 155, 186, 124
(b) 154, 187, 124
(c) 154, 185, 126
(d) 150, 140, 175
| Answer: (a) 155, 186, 124 Solution: Ration of the coins = 5 : 6 : 4 Number of 1 rupee coin = 465×515=155 Number of 50 paisa coin = 465×615=186 Number of 25 paisa coin = 465×415=124 Rules: x coins consists of 1 rupee, 50 paisa and 25 paisa coins. Their values are in the ratio a:b:c. The number of each type of coins respectively is First we convert ratio from values to number Ratio of the coins = a : 2b : 4c Number of 1 rupee coin = x×aa+2b+4c Number of 50 paisa coin = x×2ba+2b+4c Number of 25 paisa coin =x×4ca+2b+4c |
Q16. If a : b = 2 : 3, b : c = 3 : 4, c : d = 4 : 5, find a : b : c : d.
(a) 5 : 4 : 3 : 2
(b) 30 : 20 : 15 : 12
(c) 2 : 3 : 4 : 6
(d) 2 : 3 : 4 : 5
| Answer: (d) 2 : 3 : 4 : 5 Solution: a : b : c : d = 2 : 3 : 4 : 5 Trick: If A:B = m : n, B:C = n : o and C : D = o : p then A:B:C :D= m : n : o : q |
Q17. Divide Rs. 671 among A, B, C such that if their shares be increased by Rs. 3, Rs. 7 and Rs. 9 respectively, the remainder shall be in the ratio 1 : 2 : 3.
(a) Rs. 112, Rs. 223, Rs. 336
(b) Rs. 114, Rs. 221, Rs. 336
(c) Rs. 112, Rs. 227, Rs. 332
(d) Rs. 114, Rs. 223, Rs. 334
| Answer: (a) Rs. 112, Rs. 223, Rs. 336 Solution: Let A’s share be Rs. x, B’s share be Rs. y. Then, C’s share = Rs. [671 – (x + y)] Now, x + 3 : y + 7 : 671 – (x + y) + 9 = 1: 2 : 3 x + 3 : y + 7 : 680 – (x + y) = 1: 2 : 3 ⇒ x + 3 = 16×690=115 or x = 112 ⇒ y + 7 = 26×690=230 = or y = 223 ∴ C’s share = Rs. [671 – (x + y)] = 671 – 335 = 336 Using trick: After increased total share = 671 + 3 + 7 + 9 = 690 C’s share = 36×690−9=336 |
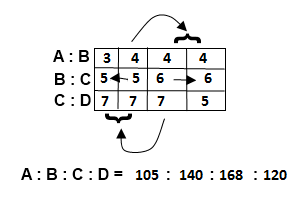
Q18. If Rs. 1066 is divided among A, B, C and D such that A : B = 3 : 4, B : C = 5 : 6 and C : D = 7 : 5, who will get the maximum?
(a) B
(b) A
(c) C
(d) D
| Answer: (c) C Solution: From ratio we can say C’s share is maximum
or A’s share = 105533×1066=210 B’s share = 140533×1066=280 C’s share = 168533×1066=336 (Maximum) D’s share = 120533×1066=240 C’s share is maximum |
Q19. The income of A and B are in the ratio 3 : 2 and expenses are in the ratio 5 : 3. If both save Rs. 200, what is the income of A?
(a) Rs. 1000
(b) Rs. 1200
(c) Rs. 1500
(d) Rs. 1800
| Answer: (b) Rs. 1200 Solution: Let income of A = Rs. 3m, income of B = Rs. 2m and expenditure of A = Rs. 5p, expenditure of B = Rs. 3p Now, saving = income – expenditure ∴ 3m – 5p = 2m – 3p = 200 ⇒ m = 2p and p = 200 ∴ m = 400 ∴ A’s income = Rs. 1200 Using Trick: Monthly income of A = 200×3(3−5)3×3−2×5=1200 |
Q20. A and B are two alloys of gold and copper prepared by mixing metals in the ratio 7 : 2 and 7 : 11 respectively. If equal quantities of the alloys are melted to form a third alloy C, the ratio of gold and copper in C will be:
(a) 5 : 7
(b) 5 : 9
(c) 7 : 5
(d) 9 : 5
| Answer: (c) 7 : 5 Solution: Gold in C in one unit = (79+718)=76 Copper in C in one unit = (29+1118)=56 Ratio of gold and copper in C = 76:56=7:5 |