Ratio and Proportion: Concept, Short Trick with Solved Example

Ratio and Proportion: Concept, Short Trick with Solved Example

Ratio: The comparative relation between two amounts/quantities of same type is called ratio.

Let an amount be x and another is y, then, the ratio between them is x : y or x/y.

Here ‘x’ is called antecedent and ‘y’ is called consequent

Mixed ratio – Let x:y and P:Q be two ratios, then Px : Qy is called mixed ratio.

Duplicate Ratio–The mixed ratio of two equal ratios is called the duplicate Ratio as

Duplicate ratio of a:b is a² : b²

Sub duplicate Ratio–The square root of a certain ratio is called its sub duplicate.

The sub duplicate ratio of a: b = $\sqrt{a}:\sqrt{b}$

Triplicate Ratio–The cube of a certain ratio is called triplicate ratio.

The triplicate ratio of a:b = a³ : b³

Sub triplicate Ratio–The cube root of a certain ratio is called sub triplicate ratio as–

The Sub triplicate Ratio of a:b = $\sqrt[3]{a}:\sqrt[3]{b}$

Inverse Ratio–The Reciprocal of quantities of ratio is called its inverse. Reciprocal or inverse ratio of a:b = $\frac{1}{a}:\frac{1}{b}\,\,or\,\,\frac{ab}{a}:\frac{ab}{b}\,\,or\,\,b:a$

Directly Proportional: If x = ky, where k is a constant, then we say that x is directly proportional to y. It is written as x ∝ y.

Inversely Proportional: If x = k/y where k is a constant, then we say that x is inversely proportional to y.

It is written as x ∝ 1/y

Proportion: When two ratios are equal to each other, then they are called proportional as

a:b = c:d, then, a, b, c and d are in proportion.

or,

a:b :: c:d

Example: 2:5 = 6: 15, then we write 2:5 :: 6:15

Example: If 8, 14, 7x + 2, 28 are proportion then find the value of x.

Solution: 8 : 14 = 7x + 2 : 28

⇒ $\frac{8}{14}=\frac{7x+2}{28}$

⇒ $7x+2 =\frac{8\times 28}{14}=16$

⇒ x = (16 – 2)/7 = 2

Fourth Proportional– Let x be the fourth proportional of a, b and c, then a:b::c:x

i.e. $\frac{a}{b}=\frac{c}{x}\,\,or\,\,x\,\,=\frac{bc}{a}$

∴ Fourth proportional of a, b and c = $\frac{bc}{a}$

Example: Find the Fourth proportional of 4, 6 and 8.

Solution: Fourth proportional = $\frac{6\times 8}{4}=12$

Third proportional–Let ‘x’ be the third proportional of a and b then, a:b :: b:x

i.e. $\frac{a}{b}=\frac{b}{x}\,\,or\,\,ax\,\,=b^2\,\,or\,\,x=\frac{b^2}{a}$

∴ Third proportional of a and b = $\frac{b^2}{a}$

Example: Find the third proportional of 4 and 6.

Solution: Third proportional = $\frac{6^2}{4}=9$

Mean Proportion – Let x be the mean proportion between a and b, then a:x::x:b (Real condition)

i.e. $\frac{a}{x}=\frac{x}{b}\,\,or\,\,x^2=ab\,\,or\,\,x\,\,=\,\,\sqrt{ab}$

∴ Mean proportional of a and b = $\sqrt{ab}$

Example: Find the third proportional of 4 and 9.

Solution: Mean proportional = $\sqrt{4\times 9}=6$

Invertendo–The proportion in which antecedent and consequent quantities change their places, is called invertendo.

Invertendo of a:b = c:d is b:a = d:c

Alternendo–If a:b ::c:d is a proportion then its alternendo is a:c::b:d. i.e. alternendo of

$\frac{a}{b}=\frac{c}{d}\,\,is\,\,\frac{a}{c}=\frac{b}{d}$

Componendo–If a:b::c:d is a proportion, then componendo is (a + b) : b :: (c + d) : d

It means, If $\frac{a}{b}=\frac{c}{d}\,\,\Rightarrow \frac{a+b}{b}=\frac{c+d}{d}$

Dividendo–If a:b :: c:d is a proportion, then its dividendo is (a – b): b:: (c – d):d

It means, If $\frac{a}{b}=\frac{c}{d}\,\,\Rightarrow \frac{a-b}{b}=\frac{c-d}{d}$

Componendo and dividendo–If there is a proportion a:b::c:d then its componendo and dividendo is (a + b):(a – b)::(c + d):(c – d)

It means, If $\frac{a}{b}=\frac{c}{d}\,\,\Rightarrow \frac{a+b}{a-b}=\frac{c+d}{c-d}$

Dividendo and Componendo –If there is a proportion a:b::c:d then its componendo and dividendo is (a – b):(a  b)::(c – d):(c + d)

It means, If $\frac{a}{b}=\frac{c}{d}\,\,\Rightarrow \frac{a-b}{a+b}=\frac{c-d}{c+d}$

Some Important rule of Ratio and proportion:

RULE 1 : Let ‘x’ be a number which is subtracted from a, b, c and d to make them proportional, then

x = $\frac{ad-bc}{\left( a-b \right) -\left( b-c \right)}$

and

Let ‘x’ be a number which is added to a, b, c and d to make them proportional, then

x = $\frac{bc-ad}{\left( a-b \right) -\left( b-c \right)}$

Example: How much added to each of 6, 8, 10 and 13 to make them proportional?

Solution: Result = $\frac{80-78}{\left( -2 \right) -\left( -3 \right)}=2$

Example-1: How much subtract from each of 13, 18, 19 and 27 to make them proportional?

Solution: Result = $\frac{351-342}{\left( -5 \right) -\left( -8 \right)}=3$

RULE 2 : If A:B = x:y and B:C = y:z then

(i) A:C = x : z

(ii) A:B:C = x : y : z

Example: If A:B = 4 : 5 and B:C = 5 : 6 then (i) A:C =  ? and (ii) A:B:C = ?

Solution: (i) A:C = 4 : 6 = 2 : 3

(ii)  A:B:C = 4 : 5 : 6

RULE 3 : If A:B = x:y and B:C = p:q then

(i) A:C = product of antecedent : product of consequent = xp : yq

(ii) A:B:C  = xp : yp : yq

It is done as follows:

A:B = x:y = xp : yp ( by multiplying p)

B:C = p:q = yp : yq ( by multiplying y)

A:B:C = xp:yp:yq

Remember this trick:

Example: If A:B = 5 : 6 and B:C = 7 : 9 then find (i) A:C and  (ii) A:B:C

Solution: (i) A:C = 5 : 9

(ii) Using trick

RULE 4 : If A:B = m : n, B:C = n : o and C : D = o : p then

(i) A:C = m : p

(ii) A:B:C :D= m : n : o : q

Example: If A:B = 5 : 6,  B:C = 6 : 7 and C : D = 7 : 8 then (i) A:C =  ? and (ii) A:B:C:D = ?

Solution: (i) A : D = 5 : 8

(ii) Using Trick

A : B : C : D = = 5 : 6 : 7 : 8

RULE 5 : If A:B = m : n, B:C = o : p and C : D = q : r then

(i) A:D = moq : npr

(ii) It is done as follows:

A : B = m : n

B : C = o : p

C : D = q : r

A : B : C : D = moq : noq : npq : npr

Remember this trick:

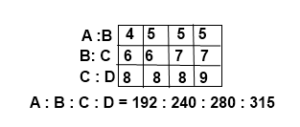
Example: If A:B = 4 : 5, B:C = 6 : 7 and C : D = 8 : 9 then find (i) A : D and (ii) A : B : C : D

Solution: (i) A : D = 192 : 315 = 64 : 105

(ii) Using trick

RULE 7 : If A : x = B : y = C : z then

(i) $\frac{A+B+C}{A}=\frac{x+y+z}{x}$

(ii) $\frac{A+B+C}{B}=\frac{x+y+z}{y}$

(iii) $\frac{A+B+C}{C}=\frac{x+y+z}{z}$

Example: If $\frac{a}{3}=\frac{b}{4}=\frac{c}{7}$ , then $\frac{a+b+c}{c}$ is equal to :

Solution: $\frac{a+b+c}{c}\,\,=\frac{3+4+7}{7}=2$

RULE 8 : If xA = yB = cZ then A: B :C then A: B :C = ?

A : B : C = $\frac{1}{\mathrm{x}}:\frac{1}{\mathrm{y}}:\frac{1}{\mathrm{z}}=\mathrm{yz}:\mathrm{xz}:\mathrm{xy}$

Example: If A of 30

Solution:  A of 30

A : B : C =  $\frac{1}{0.3}:\frac{1}{0.25}:\frac{1}{0.2}=\frac{10}{3}:4:5=10:12:15$

RULE 9 : If an amount S is to be divided between A and B in the ratio x : y then

(i) Part of A = $\frac{x}{x+y}\times S$

(ii) Part of B =  $\frac{y}{x+y}\times S$

(iii) Difference of part of A and B = $\frac{x-y}{x+y}\times S$ where x > y

Example: Abdullah and Amaan share their profit in the ratio 6:5. If their total profit is 1661 the what is their profit?

Solution: Abdullah’s Profit = $\frac{6}{11}\times 1661=906$

Amaan’s Profit = $\frac{5}{11}\times 1661=755$

RULE 10 : If the ratio of share of A and B is x : y and the difference in their share is ‘D’ then,

(i) Part of A =  $\frac{x}{x-y}\times D$

(ii) Part of B = $\frac{x}{x-y}\times D$

(iii) The sum of parts of A and B = $\frac{x+y}{x-y}\times D$ where x > y

Example:  The ratio of share of Rashid and Amit is 13:11 and their share difference is 144. Find the share of Rashid and Amit?

Solution: Rashid’s share = $\frac{13}{13-11}\times 144=936$

Amit’s share = $\frac{11}{13-11}\times 144=792$

RULE 11: If the ratio of A and B is x : y and the part of A is ‘R’, then

(i) Share of B = $\frac{y}{x}\times R$

(ii) Total share of A and B = $\frac{x+y}{x}\times R$

(iii) Difference in share of A and B = $\frac{x\sim y}{x}\times R$

Example: The ratio of daily earning of Madhu and Rahul is 7:9. If Madhu’s daily earning is Rs. 175 then what is the Rahul’s daily earning and what was their total earning?

Solution: Rahul’s daily earning = $\frac{9}{7}\times 175=225$

Their total earning = $\frac{7+9}{7}\times 175=400$

RULE 12 : If Addition of two number ‘S’ and their difference is ‘D’ the ratio of the two number

Ratio = (S +D) : (S –D)

Example: Sum of two number is 145 and their difference is 25. Find the ratio of two numbers?

Solution: ratio of the two number = 145 + 25 : 145 – 25 = 17:12

RULE 13 : If the amount S is divided among A, B and C in the ratio x : y : z, then

(i) The share of A = $\frac{xS}{x+y+z}$

(ii) The share of B =$\frac{yS}{x+y+z}$

(iii) The share of C =$\frac{zS}{x+y+z}$

Example: If Rs. 782 be divided into three part, proportional to  $\frac{1}{2}:\frac{2}{3}:\frac{3}{4}$ then the first part is

Solution: $\frac{1}{2}:\frac{2}{3}:\frac{3}{4}\,\,=6:8:9$

First part = $\frac{6\times 782}{23}=204$

Rule 14: The ratio of three number is x : y : z and their product is ‘P’. The numbers are:

1^st Number = $x\times \sqrt[3]{\frac{P}{xyz}}$

2nd Number = $y\times \sqrt[3]{\frac{P}{xyz}}$

3rd Number = $z\times \sqrt[3]{\frac{P}{xyz}}$

Example: The ratio of three number is 3 : 4 : 7 and their product is 18144. The numbers are:

Solution: 1^st Number = $3\times \sqrt[3]{\frac{18144}{3\times 4\times 7}}=18$

2nd Number = $4\times \sqrt[3]{\frac{18144}{3\times 4\times 7}}=24$

3rd Number = $7\times \sqrt[3]{\frac{18144}{3\times 4\times 7}}=42$

RULE 15: If the ratio of A, B and C is x : y : z and the part of A is ‘D’ then,

(i) Part of B = $\frac{y}{x}\times D$

(ii) Part of C = $\frac{z}{x}\times D$

Example: The income of A, B and C are in the ratio 3 : 7 : 4. If income of A is Rs.2400 then what is income of B and C?

Solution: Income of B = $\frac{7}{3}\times 2400=5600$

Income of C = $\frac{4}{3}\times 2400=3200$

RULE 16: If an amount is to be divided among A, B and C in the ratio x : y : z and the difference between A and B is share is  ‘D’, then

(i) Part of C = $\frac{z}{x\sim y}\times D$

Example: The income of A, B and C are in the ratio 7 : 9 : 12 and Difference of income of A and B is Rs.560. Find C income?

Solution: C’s income = $\frac{12}{9-7}\times 560=3360$

RULE 17 : If the ratio of allegation of milk and water in a glass is m:n and in other glass allegation is p:q, then the ratio of milk and water in third glass which contains allegation of both glasses is

Ratio = $\left( \frac{m}{m+n}+\frac{p}{p+q} \right) :\left( \frac{n}{m+n}+\frac{q}{p+q} \right)$

Example: Two equal glasses filled with alcohol and water in the proportions 2 : 1 and 3 : 2 are emptied into a third glass. The proportion of alcohol and water in the third glass will be

Solution: Ratio = $\frac{2}{2+1}+\frac{3}{3+2}:\frac{1}{2+1}+\frac{2}{3+2}$

= $\frac{2}{3}+\frac{3}{5}:\frac{1}{3}+\frac{2}{5}=\frac{19}{15}:\frac{11}{15}=19:11$

RULE 18 : If the ratio of milk and water in the allegation of A liter is m:n then water must be added in it so that ratio of milk and water would be p:q is

Required amount of water = $\frac{A\left( mq-np \right)}{p\left( m+n \right)}$

Example: In a mixture of 60 liters, the ratio of milk and water is 2 : 1. How much more water must be added to make its ratio 1 : 2?

Solution: Required amount of water = $\frac{60\left( 4-1 \right)}{1\left( 3 \right)}=60$

RULE 19: The ratio of income of two persons A and B is m:n. If the ratio of their expenditures is p:q, then the monthly income of A and B, when each one of them saves ‘S’ rupees will be

Monthly income of A = $\frac{Sm\left( q-p \right)}{mq-np}$

Monthly income of B =$\frac{Sn\left( q-p \right)}{mq-np}$

Example: A and B have monthly incomes in the ratio 5 : 6 and monthly expenditures in the ratio 3 : 4. If they save Rs.2550, find the monthly income of B:

Solution: Monthly income of A =$\frac{2550\times 5\times 1}{20-18}=6375$

Monthly income of B =  $\frac{2550\times 6\times 1}{20-18}=7650$

RULE 20: Two numbers are in the ratio a:b and if each number is increased by x, the ratio becomes c:d. Then the two numbers will be

$\frac{ax\left( c-d \right)}{ad-bc}\,\,and\,\,\frac{bx\left( c-d \right)}{ad-bc}$

Difference of the Number =  $\frac{\mathrm{x}\left( \mathrm{a}-\mathrm{b} \right) \left( \mathrm{c}-\mathrm{d} \right)}{\mathrm{ad}-\mathrm{bc}}$ [Take positive value]

Sum of the Numbers = $\frac{\mathrm{x}\left( \mathrm{a}+\mathrm{b} \right) \left( \mathrm{c}-\mathrm{d} \right)}{\mathrm{ad}-\mathrm{bc}}$

Example: The present ages of A and B are in the ratio 3 : 4. Ten years ago, this ratio was 4 : 7. The present ages of A and B are respectively:

Solution:  10 years ago A’s Age = $\frac{4\times 10\times -1}{16-21}=8$

The present ages of A = 10 + 8 =18

10 years ago B’s Age = $\frac{7\times 10\times -1}{16-21}=14$

The present ages of B = 14 + 10 = 24

Example-2: The present ages of Father and Son are in the ratio 7:2. Eight years later ratio of their age is 5 : 2. What is The present ages of Father and Son?

Solution: Father’s age = $\frac{7\times 8\times 3}{14-10}=42$

Son’s age = $\frac{2\times 8\times 3}{14-10}=12$

Example-3: If two numbers are in the ratio 2 : 3 and the ratio becomes 3 : 4 when 8 is added to both the numbers, then the sum of the two numbers and difference of the numbers is:

Solution: Sum of the Numbers = $\frac{8\left( 2+3 \right) \left( 3-4 \right)}{8-9}=40$

Difference of the numbers = $\frac{8\left( 2-3 \right) \left( 3-4 \right)}{8-9}=8$(since difference, we take positive value)

First number = $\frac{2\times 8\times \left( 3-4 \right)}{8-9}=16$

Second Number = $\frac{3\times 8\times \left( 3-4 \right)}{8-9}=24$

RULE 21: Two numbers are in the ratio a:b and if x is subtracted from each number the ratio becomes c:d. The two numbers will be

$\frac{ax\left( d-c \right)}{ad-bc}\,\,and\,\,\frac{bx\left( d-c \right)}{ad-bc}$

Difference of the number = $\frac{\mathrm{x}\left( \mathrm{a}-\mathrm{b} \right) \left( \mathrm{d}-\mathrm{c} \right)}{\mathrm{ad}-\mathrm{bc}}$ [Take positive value]

Sum of the Numbers = $\frac{\mathrm{x}\left( \mathrm{a}+\mathrm{b} \right) \left( \mathrm{d}-\mathrm{c} \right)}{\mathrm{ad}-\mathrm{bc}}$

Example: Two numbers are in the ratio 5 : 7. On diminishing each of them by 40, they become in the ratio 17 : 27. The difference of the numbers and sum of the numbers is:

Solution: Difference of the number = $\frac{40\left( 5-7 \right) \left( 27-17 \right)}{5\times 27-7\times 17}=50$

Sum of the Numbers = $\frac{40\left( 5+7 \right) \left( 27-17 \right)}{5\times 27-7\times 17}=300$

First number = $\frac{5\times 40\times \left( 27-17 \right)}{5\times 27-7\times 17}=125$

Second Number = $\frac{7\times 40\times \left( 27-17 \right)}{5\times 27-7\times 17}=175$

 Rules 22: x numbers of coins consists of 1 rupee, 50 paisa and 25 paisa coins in a bag. The ratio of their rupee values being a: b : c. The number of each type of coins are present in the bag:

Number of 1 rupee coin = $\mathrm{x}\times \frac{\mathrm{a}}{\mathrm{a}+2\mathrm{b}+4\mathrm{c}}$

Number of 50 paisa coin = $\mathrm{x}\times \frac{2\mathrm{b}}{\mathrm{a}+2\mathrm{b}+4\mathrm{c}}$

Number of 25 paisa coin =$\mathrm{x}\times \frac{4\mathrm{c}}{\mathrm{a}+2\mathrm{b}+4\mathrm{c}}$

Example: A box contains 315 coins in rupee, 50 paisa and 25 paisa coins. The ratio of their rupee values being 13 : 11 : 7. The number of each type of coins are present in the box:

Solution:

Number of 1 rupee coin = $315\times \frac{13}{13+2\times 11+4\times 7}=65$

Number of 50 paisa coin = $315\times \frac{22}{13+2\times 11+4\times 7}=110$

Number of 25 paisa coin =$315\times \frac{28}{13+2\times 11+4\times 7}=140$

Rules 23: ‘x’ Rupees consists of 1 rupee, 50 paisa and 25 paisa coins in a bag. Ratio of the coin is a: b : c. The number of each type of coins present in the bag

Number of 1 rupee coin = $\mathrm{x}\times \frac{1\times 4\mathrm{a}}{4\mathrm{a}+2\mathrm{b}+\mathrm{c}}$

Number of 50 paisa coin = $\mathrm{x}\times \frac{2\times 2\mathrm{b}}{4\mathrm{a}+2\mathrm{b}+\mathrm{c}}$

Number of 25 paisa coin = $\mathrm{x}\times \frac{4\times \mathrm{c}}{4\mathrm{a}+2\mathrm{b}+\mathrm{c}}$

Example: In a bag, there are three types of coins — 1-rupee, 50 paisa and 25-paisa in the ratio of 3 : 8 : 20. Their total value is 372. The total number of coins is

Solution:

Number of 1 rupee coin = $372\times \frac{12}{12+16+20}=93$

Number of 50 paisa coin = $372\times \frac{2\times 16}{12+16+20}=248$

Number of 25 paisa coin = $372\times \frac{4\times 20}{12+16+20}=620$

The total number of coins = 93 + 248 + 620 = 961

Practice: Ratio and Proportion MCQ Question