Ratio and Proportion MCQ Question with Details Solution |
Read: Concept and Short Trick |
Q1. If P:Q = 8:15 and Q:R = 3:2, then find P:Q:R.
(a) 8:15:7
(b) 7 : 15 : 8
(c) 8: 15: 10
(d) 10 : 15 : 8
(e) None of the above
| Answer: (c) 8: 15: 10 Solution: P:Q = 8:15 and Q:R = 3:2 = 15:10 Now P:Q:R= 8:15:10 Using Trick-1:
Using Trick-2:
|
Q2. If A : B = 6 : 7, B : C = 8 : 9 and C : D = 5 : 11 then the value of A : D = ?
(a) 80:251
(b) 90: 257
(c) 80: 253
(d) 75: 262
| Answer: (a) 80:251 Solution: AB=67,BC=89andCD=511 Multiplying them AB×BC×CD=67×89×511=80231 ∴ A:D = 80:231 Using Trick: A:D = product of antecedent : product of consequent = 240:693 = 80:251 |
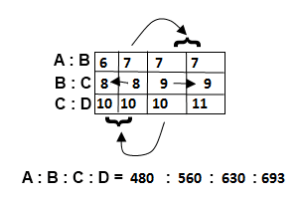
Q3. If A : B = 6 : 7, B : C = 8 : 9 and C : D = 10 : 11 then the value of A:B:C:D = ?
(a) 48 : 80 : 99
(b) 80 : 56 : 99
(c) 60 : 70 : 77
(d) 560 : 630 : 693
| Answer: (d) 560 : 630 : 693 Solution: First we made B same for first two ratio and C same for last two ratio. A : B = 6 : 7 = 6 × 8 × 10 : 7 × 8 × 10; B : C = 8 : 9 = 8 × 7 × 10 : 9 ×7 ×10 ; C : D = 10 : 11 = 10 × 7 × 9 : 11 × 7 × 9 A : B : C : D = 6 × 8 × 10 : 7 × 8 × 10 : 9 ×7 ×10 : 11 × 7 × 9 = 480:560:630:693 Using trick:
|
Q4. If A : B = 2: 3, B : C = 5: 7 and C : D = 3:10, then what is A : D equal to?
(a) 1 : 7
(b) 2 : 7
(c) 1 : 5
(d) 5 : 1
| Answer: (a) 1 : 7 Solution: A : B = 2: 3, B : C = 5: 7 and C : D = 3:10 ∴ AD=AB×BC×CD = 23×57×310=17 ∴ A:D = 1:7 Using Trick: A:D = product of antecedent : product of consequent = 2×5×3:3×7×10 = 1:7 |
Q5. Find the 4th proportional to 4, 16 and 7.
(a) 28
(b) 29
(c) 22
(d) 25
(e) None of the above
| Answer: (a) 28 Solution: Let 4th proportional = x ∴ 416=7x ⇒ 4x = 16×7 ⇒x = 28 |
Q6. Calculate the 3rd proportional to 15 and 30.
(a) 55
(b) 15
(c) 65
(d) 60
(e) None of the above
| Answer: (d) 60 Solution: Let 3rd proportional = x ∴ 15:30 :: 30: x ⇒ 1530=30x ⇒ 15x = 900 ⇒x = 60 |
Q7. Find the mean proportional between 9 and 64.
(a) 25
(b) 24
(c) 27
(d) 35
(e) None of the above
| Answer: (b) 24 Solution: mean proportional = √9×64=24 Mean Proportion – Let x be the mean proportion between a and b, then a:x::x:b (Real condition) i.e. ax=xborx2=aborx=√ab ∴ Mean proportional of a and b = √ab |
Q8. What will be the inverse ratio of 17 : 19?
(a) 19 : 17
(b) 18 : 17
(c) 17 : 18
(d) 19 : 5
(e) None of the above
| Answer: (a) 19 : 17 Solution: inverse ratio = 19 : 17 |
Q9. If 4a = 5b and 7b = 9c, then a: b: c is equal to
(a) 45 : 36 : 28
(b) 44 : 33 : 28
(c) 28 : 36 : 45
(d) 36 : 28 : 45
(e) None of the above
| Answer: (a) 45 : 36 : 28 Solution: 4a = 5b ⇒ a : b = 5:4 and 7b = 9c ⇒b:c = 9:7
|
Q10. If 1a:1b:1c=2:3:5 then the value of a : b : c
(a) 6 : 15 : 10
(b) 3 : 15 : 10
(c) 15 : 3 : 10
(d) 15 : 10 : 6
| Answer: (d) 15 : 10 : 6 Solution: Let ratio constant k 1a:1b:1c=2:3:5 1a=2k⇒a=12k 1b=3k⇒b=13k 1c=2k⇒c=13k a : b : c = 12k:13k:15k=15:10:6 = 5:3:2 |