CTET 2014 February Paper-1 Question with Answer | ||
| Child Development | Mathematics | EVS |
| Language – I (Eng) | Language – II (Hindi) | |
Mathematics
DIRECTIONS: Answer the following questions by selecting the most appropriate option
Q31. The perimeter of a square is 20 cm. A rectangle has the same width as the square. The length of the rectangle is double its width. The area, in square cm, of the rectangle is
(a) 30
(b) 50
(c) 100
(d) 25
| Answer: (b) 50 Solution: perimeter of square = 20 cm Let, side of square = x, then 4x = 20 ⇒ x = 5 ∴ Length of rectangular = 2x = 10 ∴ Area of rectangular = 10 × 5 = 50 cm2 |
Q32. The internal length, breadth, and height of a rectangular box A are 20 cm, 18 cm, and 15 cm respectively and that of box B are 18 cm, 12 cm, and 5 cm respectively the volume of box A is how many times that of box B?
(a) 4
(b) 5
(c) 6
(d) 3
| Answer: (b) 5 Solution: volume of box B = 18 × 12 × 5 = 1080 cm3 Volume of box A = 20 × 18 × 15 = 5400 cm3 = 5 × 1080 cm3 ∴ the volume of box A is 5 times that of box B |
Q33. Which of the following is not correct?
(a) Area of a square of side 10 cm = Area of a rectangle of length 10 cm and breadth 0.1 m
(b) 1 meter 5 centimeter = 1.5 m
(c) 0.40 is same as 0.4
(d) Rupee 3/4 = Rupee 0.75
| Answer: (b) 1 meter 5 centimeter = 1.5 m Solution: 1 meter 5 centimeter = 1 m + 0.05 m = 1.05 m So, (b) is incorrect. |
Q34. One orange costs five and a half rupees and one kg apple costs 80. Then the total cost of one and half dozen of oranges and one and three-fourth kg of apples is
(a) 219
(b) 229
(c) 239
(d) 209
| Answer: (c) 239 Solution: Total cost = 18 × 5.5 + 134 × 85 = 99 + 140 = 239 |
Q35. NCF, 2005 states that Mathematics teaching should be ambitious, coherent and important. Here, ‘ambitious’ refers to the achievement of
(a) Narrow goals of Mathematics
(b) Linking of Mathematics with other subjects
(c) Application of Mathematics
(d) Higher goals of Mathematics
| Answer: (d) higher goals of Mathematics |
Q36. In Class, I, the concept of even number and the odd number was introduced by the activity of pairing the given number with concrete objects. Then the teacher asked the students to check
(i) Whether the total number of crayons in their color boxes is even in number or odd in number.
(ii) Whether the number of pages in their Math notebook is odd or even. This task of finding even or odd number of crayons/pages is
(a) Assessment for learning
(b) Assessment as learning
(c) Assessment at the end of learning
(d) Assessment of learning
| Answer: (a) assessment for learning |
Q37. After explaining the operation of subtraction in Class II, the teacher drew the following diagram on the board and asked the students to fill in the circles: The purpose of the exercise is
(a) Strengthening the skill of addition and subtraction
(b) Summative assessment
(c) Arranging fun activity for the students
(d) The mathematization of mind.
| Answer: (a) strengthening the skill of addition and subtraction |
Q38. How many rectangles are there in the following figure?
The above question is testing
(a) Knowledge of learner
(b) Understanding of learner
(c) Creativity of leaner
(d) Memory of learner
| Answer: (b) understanding of learner |
Q39. Which of the following activities is meant to enhance the problem-solving abilities of students of Class I
(a) A crossword puzzle containing clues for all key terms learned to like even number, an odd number, and a composite number, prime
(b) A group project how the students of the primary wing shall be distributed equally in four houses (house system of school) so that every house has talented students from sports, arts, cultural and academic activities?
(c) Conduct an interclass quiz in the class on ‘numbers
(d) A worksheet containing problems on four basic operations like Find 25×34, 451, etc.
| Answer: (b) A group project how the students of the primary wing shall be distributed equally in four houses (house system of school) so that every house has talented students from sports, arts, cultural and academic activities? |
Q40. The recommended key concept in the unit of multiplication in Class III is
(a) Multiplication of 2-digit number with a 2-digit number
(b) Properties of multiplication – order property and group
(c) Word problem based on multiplication
(d) Multiplication 3-digit numbers by 10
| Answer: (b) properties of multiplication – order property and group |
Q41. From the unit of fraction, the teacher asks the student to list any five fractions
This question refers to
(a) Higher level of thinking
(b) Analytical thinking
(c) Spatial thinking
(d) Lower level of thinking
| Answer: (d) lower level of thinking |
Q42. In an exercise, the question was Measure the lengths of the line segments
![]() and
and ![]()
The child answered- length of AB = 5 cm, length of AB = 3 cm
This is referred to
(a) Conceptual error
(b) Procedural error
(c) Error due to the habit of naming a line segment as AB
(d) Reading error
| Answer: (c) error due to the habit of naming a line segment as AB |
Q43. A teacher distributed a newspaper in Class V and asked the students to read the cricket scores of the Indian team in the latest match. Then she asked them to drawbar graph of the scores the teacher is trying to
(a) Help the students to make connections between mathematical concepts and real life
(b) Teach them through a project approach
(c) Make the class joyful and communicating
(d) Enhance the reasoning power of the students
| Answer: (a) help the students to make connections between mathematical concepts and real life |
Q44. The following word problem was given to a child of Class IV Mumbai has 356 bus stops. Delhi has 127 more bus stops than Mumbai. How many bus stops are there in all, in Delhi? The child’s response to the above problem is recorded as
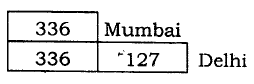
Total bus stops in Delhi are 336 +127 = 463
The teacher shall report about his performance as
(a) The child can find the answer correctly but his expression is poor
(b) The child is good at visualizing and analyzing, and his problem-solving ability is appreciable
(c) The child has not adopted the right procedure. He n to practice more
(d) The child is not able to write all steps required properly
| Answer: (b) the child is good at visualizing and analyzing, and his problem-solving ability is appreciable |
Q45. A student was asked to read the following numbers
306,408, 4008, 4010
He read as follows
Thirty-six, forty-eight, four hundred eight, forty ten
The reason for the error in reading is that
(a) The student does not like Math class and finds the class boring
(b) The student has understood the concept of place value but does not know how to use it
(c) The student is not fit for the study of Math
(d) The student is not able to understand the concept of place value and feels comfortable using two-digit numbers only
| Answer: (d) the student is not able to understand the concept of place value and feels comfortable using two-digit numbers only |
Q46. The parameter(s) of assessment for time’ for Class IV shall be
(a) Reading the time on the analogous clock only
(b) Reading the time on the digital and analogous clock, the concept of half past, quarter past, quarter to, a.m., p.m., the relation between minutes and seconds
(c) Reading the time on a digital clock, the concept of a.m. and p.m.
(d) Reading the time on the digital clock only
| Answer: (b) reading the time on the digital and analogous clock, the concept of half past, quarter past, quarter to, a.m., p.m., the relation between minutes and seconds |
Q47. The tall shape of Mathematics mentioned in NCF, 2005 refers to
(a) Solving challenging problems
(b) Creating a Math game
(c) Providing hands-on experience
(d) The building of one concept on other
| Answer: (d) the building of one concept on other |
Q48. Consider the following
5 + 3 =?
The open-ended question corresponding to the above close-ended question is
(a) Find the sum of 5 and 3
(b) What shall be added to 5 to get 8?
(c) Give any two numbers whose sum is 8
(d) What is the sum of 5 and 3?
| Answer: (c) Give any two numbers whose sum is 8 |
Q49. Farhan went to the school library and found that 100 books kept in the story section are spoiled. 20 books are missing. 219 are kept on a shelf and 132 were issued to students. How many storybooks were there in the library?
The teacher can teach the following value through this question
(a) Helping others
(b) Sharing books with others
(c) Taking good care of books
(d) Sense of cooperation
| Answer: (c) Taking good care of books |
Q50. The product of the place values of 5 and 6 in 70560 is
(a) 300
(b) 3000
(c) 30000
(d) 30
| Answer: (c) 30000 Solution: Place value of ‘5’ = 500 Place value of ‘6’ = 60 ∴ Product = 500 × 60 = 30000 |
Q51. When 3010301 is divided by 43, the quotient is
(a) 70707
(b) 70007
(c) 7077
(d) 7007
| Answer: (b) 70007 Solution: 3010301/43 = 70007 |
Q52. What should be subtracted from the product 3001 × 101 to get 300311?
(a) 2790
(b) 2090
(c) 2970
(d) 270
| Answer: (c) 2970 Solution: Let x will be subtracted ∴ 3001 × 101 – x = 300311 ⇒ x = 303101 – 300311 = 2790 |
Q53. (Smallest common multiple of 36 and 60) ÷ (Biggest common factor of 18 and 45) is equal to
(a) 20
(b) 30
(c) 40
(d) 10
| Answer: (a) 20 Solution: LCM of 36 and 60 = 180 and HCF of 18 and 45 = 9 ∴ required answer = 180 ÷ 9 = 20 |
Q54. (10 tens+11 hundred 12 ones) equals
(a) 1213
(b) 111012
(c) 101112
(d) 1212
| Answer: (d) 1212 Solution: 10 tens+11 hundred 12 ones = 100 + 1100 + 12 = 1212 |
Q55. The number of factors of 42 is
(a) 7
(b) 8
(c) 9
(d) 6
| Answer: (b) 8 Solution: factors of 42 = 1, 2, 3, 6, 7, 14, 21, 42 ∴ Number of factors = 8 |
Q56. When 3488 is divided by 12 and 2478 is divided by 11, the difference between the remainders in both cases is
(a) 5
(b) 6
(c) 7
(d) 3
| Answer: (a) 5 Solution: 3488 is divided by 12 remainder = 8 2478 is divided by 11 remainder = 3 The difference = 8 – 3 = 5 |
Q57. A train leaves station P at 8:18 a.m. and reaches station Q at 10:28 p.m. on the same day. The time taken by the train to reach Q is
(a) 14 hours 10 minutes
(b) 14 hours 46 minutes
(c) 18 hours 46 minutes
(d) 13 hours 10 minutes
| Answer: (a) 14 hours 10 minutes Solution: leaves station P at 8:18 a.m. and reached at 10:28 p.m. or 22:28 ∴ Time taken = 22:28 – 8:18 = 14 hr 10 min |
Q58. 14 L 280 ml of orange juice and 18 L 830 ml of carrot juice were mixed together. This mixture was filled in 15 bottles each containing 1.5 L. How much mixture was left?
(a) 11L 105 ml.
(b) 9L 610 ml
(c) 10L 610 ml
(d) 11 L 605 ml
| Answer: (c) 10L 610 ml Solution: Total mixtures = 14.280 l + 18.830 l = 33.11 l Total mixture filled in bottle = 15 × 1.5 = 22.5 l Mixture was left = 33.11 – 22.5 = 10.61 = 10 lit 610 ml |
Q59. One-fourth of a pizza was eaten by Renu. The rest was equally distributed among 12 children. What part of the pizza did each of these children get?
(a) 1/16
(b) 1/32
(c) 3/16
(d) 1/8
| Answer: (a) 1/16 Solution: Pizza remain after eaten by Renu = 3/4 ∴ each children get =34÷12=116 |
Q60. The number of seconds in 6 hours equals the number of minutes in
(a) 4 days
(b) 10 days
(c) 15 days
(d) 2 days
| Answer: (c) 15 days Solution: number of seconds in 6 hours = 6 × 60 × 60 = 21600 Number of minutes in day = 24 × 60 = 1440 ∴ required day = 216001440=15 |
